Олимпиадная задача: как построить ортоцентр треугольника с помощью циркуля
Задача
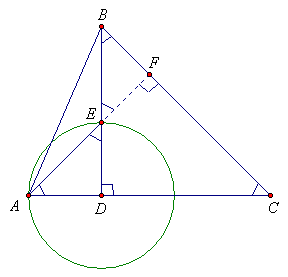
В треугольнике ABC высота BD образует со стороной BC угол в 45°. Считается, что прямая BD, содержащая высоту, уже построена. Как одним движением циркуля построить ортоцентр треугольника ABC?
Решение
Для построения достаточно из точки D провести окружность с радиусом DA. Точка пересечения K с прямой BD и будет ортоцентром треугольника. Действительно, в равнобедренном прямоугольном треугольнике KDA ∠KAD = ∠AKD = 45°. Пусть L – точка пересечения AK и BD. Тогда ∠BKL =∠AKD = 45°, кроме того, по условию ∠CBD = 45°, следовательно, AL ⊥ BC. Заметим, что построение не зависит от того, является угол ABC острым, прямым или тупым.

Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет