Олимпиадная задача: 12 точек в равногранном тетраэдре, сфера и высоты граней

Рассмотрим равногранный тетраэдр ABCD . Пусть O1— ортогональная проекция центра O описанной сферы на плоскость ABC , DD1— высота тетраэдра, M1— точка пересечения медиан треугольника ABC , H1— точка пересечения высот треугольника ABC . Тогда O1— центр описанной окружности треугольника ABC Точки O1, M1и H1лежат на одной прямой — прямой Эйлера треугольника ABC . При этом точка M1лежит между O1и H1и M1H1=2M1O1. Поскольку тетраэдр равногранный, центр O его описанной сферы совпадает с точкой M пересечения медиан, значит, точка O1лежит на проекции медианы DM1тетраэдра на плоскость ABC , т.е. на прямой D1M1. Но точки O1и M1лежат на прямой Эйлера треугольника ABC , значит, на этой прямой лежит и точка D1. Обозначим M1O1=t . Тогда

M1H1=2t, O1D1=3O1M1=3t, O1H1=M1O1+M1H1=t+2t=3t=O1D1,

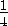следовательно, M1— середина стороны D1H1треугольника OD1H1, а т.к. OO1— высота этого треугольника и OO1=DD1=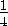 , где h — высота тетраэдра, то

OD1=OH1== .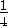

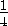Пусть K — середина высоты DD1, P — проекция точки O на прямую DD1. Тогда

PD1=OO1=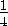, KP=KD1-PD1=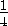-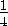= 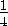, OP=O1D1=3t.

Из прямоугольного треугольника OPK находим, что

OK = = .

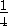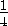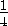Таким образом, точки D1, H1и K удалены от точки O на одно и то же расстояние , следовательно, они лежат на сфере с центром O и радиусом 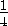. Поскольку все высоты равногранного тетраэдра равны и все его грани равны, то расстояния от точки O до остальных девяти из указанных в условии точек также равны 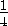. Отсюда следует утверждение задачи.

Ответ задачи отсутствует