Олимпиадная задача о минимуме частного на плоскости для квадрата ABCD.
Задача
На плоскости дан квадрат ABCD . Найдите минимум
частного 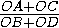 , где O — произвольная
точка плоскости.
, где O — произвольная
точка плоскости.
Решение
Известно, что для любого прямоугольника ABCD и
любой точки O в плоскости этого прямоугольника OA2+OC2=OB2+OD2.
Докажем, что 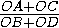
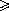
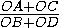 ,
или
,
или 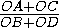 (OA+OC)
(OA+OC) 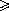 OB+OD .
Действительно,
OB+OD .
Действительно,
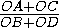 (OA+OC)
(OA+OC) 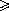 OB+OD
OB+OD 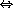 (
(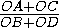 (OA+OC))2
(OA+OC))2 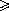 (OB+OD)2
(OB+OD)2
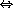
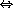 2(OA2+2OA· OC+OC2)
2(OA2+2OA· OC+OC2) 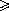 OB2+2OB· OD+OD2
OB2+2OB· OD+OD2
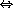
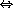 OB2+4OA· OC+OC2
OB2+4OA· OC+OC2 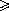 2OB· OD.
2OB· OD.
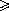 2OB· OD .
Если точка O совпадает с вершиной A , получим, что
2OB· OD .
Если точка O совпадает с вершиной A , получим, что 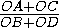 AC = 2AB , или
AC = 2AB , или
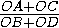 =
=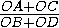 =
= 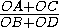 =
=
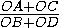 ,
,
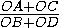 достигается.
Следовательно, минимальное значение дроби
достигается.
Следовательно, минимальное значение дроби 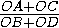 равно
равно 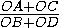 .
.
Ответ
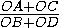 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет