Олимпиадная задача по планиметрии для 8-9 классов: периметр внутреннего пятиугольника
Задача
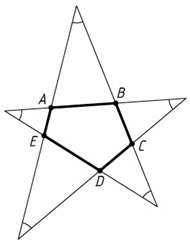
Замкнутая пятизвенная ломаная образует равноугольную звезду (см. рис.).
Чему равен периметр внутреннего пятиугольника ABCDE, если длина исходной ломаной равна 1?
Решение
Пусть K, L, M, N и O – вершины звезды, лежащие против сторон соответственно AB, BC, CD, DE и EA внутреннего пятиугольника ABCDE. Как известно, сумма углов пятиконечной звезды равна 180° (см. задачу 53380). Поскольку углы при вершинах равны, то каждый из них равен 36°. По теореме о внешнем угле треугольника ∠KBA = 72°. Отсюда следует, что треугольники AKB, BLC, CMD, DNE и AOE – равнобедренные, с углами 36°, 72°, 72°. Следовательно, AB = 2KA sin 18° = (KA + KB) sin 72°.
Сложив эти равенства, получим
AB + BC + CD + DE + EA = (KA + KB + LB + LC + MC + MD + ND + NE + OE + OA) sin 18° = (1 – AB – BC – CD – DE – EA) sin 18°, следовательно,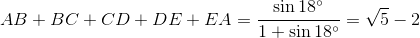 
(мы воспользовались известным равенством 
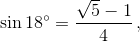см. задачу 156881).
Ответ
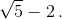
Чтобы оставлять комментарии, войдите или зарегистрируйтесь