Задание олимпиады по планиметрии для 8–9 классов: центр окружности в параллелограмме

Задача

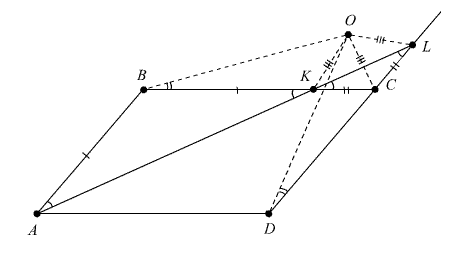
В параллелограмме ABCD, не являющемся ромбом, проведена биссектриса угла BAD. K и L – точки её пересечения с прямыми BC и CD соответственно. Докажите, что центр окружности, проведённой через точки C, K и L, лежит на окружности, проведённой через точки B, C и D.

Решение

Можно считать, что AB < BC. Пусть O – центр описанной окружности треугольника CKL.

∠KLC= ∠KAB= ∠KAD= ∠LKC, значит, треугольникиABKиKCL– равнобедренные. Поэтому равнобедренные треугольникиKCOиCLOравны (по трём сторонам). Следовательно, треугольникиBKOиDCOравны (по двум сторонам и углу: ∠BKO= 180° – ∠CKO= 180° – ∠LCO= ∠DCO). Значит, и ∠OBC= ∠OBK= ∠ODC. ТочкиBиDнаходятся по одну сторону от прямойCO(CO– биссектриса внешнего углаCтреугольникаBCD), следовательно, точки B,O,C,D лежат на одной окружности.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: Биссектриса в параллелограмме, окружности и центр

Задача

Решение

Ответ

Подтверждение удаления