Назад

Олимпиадная задача по планиметрии: параллелограмм в треугольнике для 8–9 классов

Задача 215638 • Сложность: 2 • 8-9 класс
Задача

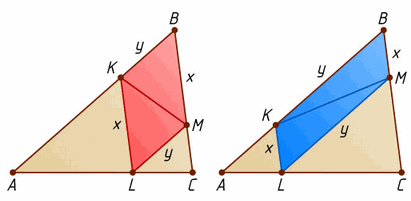
В треугольник ABC со сторонами  AB = 18  и  BC = 12  вписан параллелограмм BKLM, причём точки K, L и M лежат на сторонах AB, AC и BC соответственно. Известно, что площадь параллелограмма составляет 4/9 площади треугольника ABC. Найдите стороны параллелограмма.

Разделы:
Многочлены Планиметрия
Источники:
Система задач по геометрии Р.К.Гордина (zadachi.mccme.ru) Интернет-ресурсы
Количество версий:
4
Решение

Обозначим  BM = KL = x,  BK = LM = y,  SABC = S.  Тогда  SBKLM = 4S/9,  2S/9 = ½ SBKLM = SBKM = x/12·y/18 S,  то есть  xy = 48.  Треугольник AKL подобен треугольнику ABC, поэтому  KL : BC = AK : AB,  или  x/12 = 18–y/18,  откуда  3x + 2y = 36.  Из системы  xy = 48,  3x + 2y = 36  находим, что  x = 8,  y = 6  или  x = 4,  y = 12.

Ответ

8, 6 или 4, 12.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет