Олимпиадная задача по планиметрии: площадь треугольника внутри трапеции для 8-9 классов

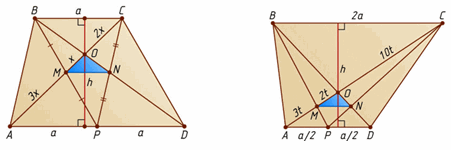
  Пусть  AD = 2BC  (рис. слева). Тогда  S_ACD : S_BAC = 2 : 1,  то есть  S_ACD = ⅔ S_ABCD = 270,  S_AОD = ⅔ SACD = 180.

  Четырёхугольники ABCP и BCDP – параллелограммы, поэтому M и N – середины BP и CP.   Так как  OA : OC = 2 : 1,  то  OM : OA = 1 : 4.  Аналогично  ON : OD = 1 : 4.

  Значит, треугольники MON и AOD подобны с коэффициентом ¼. Следовательно,  S_MON = ¹/₁₆ S_AOD = ⁴⁵/₄.

  В случае, когда  BC= 2AD   (рис. справа),  S_ACD= ⅓S_ABCD= 135, S_AОD= ⅓S_ACD= 45.   ТреугольникAMP– треугольникуCMBс коэффициентом ¼. Значит,  AM= ⅕AC= ⅗AO,  то есть  OM:OA= 2 : 5.  Аналогично  ON:OD= 2 : 5.  Следовательно,  S_MON=⁴/₂₅S_AOD=³⁶/₅.

⁴⁵/₄ или ³⁶/₅.