Олимпиадная задача по планиметрии: Внутри выпуклого четырёхугольника, 8-9 класс
Задача
Внутри выпуклого четырёхугольника ABCD взята такая точка P, что ∠PBA = ∠PCD = 90°. Точка M – середина стороны AD, причём BM = CM.
Докажите, что ∠PAB = ∠PDC.
Решение
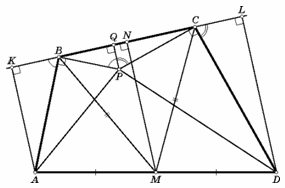
Проведём перпендикуляры AK, DL, MN и PQ – к прямой BC (см. рис.). KN = NL, а BN = NC. Следовательно, KB = CL. Заметим, что прямоугольные треугольники AKB и BQP подобны. Аналогично подобны прямоугольные треугольники CLD и PQC.
Отсюда BP : AB = QP : AB = QP : CL = CP : CD, то есть прямоугольные треугольники ABP и DCP тоже подобны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет