Олимпиадная задача по планиметрии: медианы и высоты в неравнобедренном треугольнике
Задача
В неравнобедренном треугольнике две медианы равны двум высотам. Найдите отношение третьей медианы к третьей высоте.
Решение
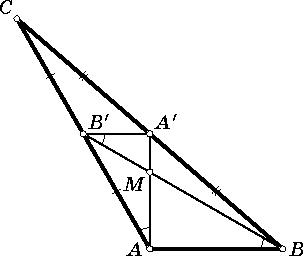
Пусть в треугольнике ABC выполнено неравенство 1 = AB < AC < BC. Тогда медиана AA' равна высоте, опущенной из вершины B, а медиана BB' – высоте, опущенной из вершины C. Значит, расстояние от точки A' до прямой AC равно половине AA', то есть ∠A'AC = 30°. Аналогично ∠B'BA = 30°.
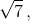 и значит, медиана из вершиныCравна
и значит, медиана из вершиныCравна 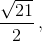 а высота из вершины Aравна
а высота из вершины Aравна 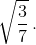
Ответ
7 : 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет