Назад

Олимпиадная задача по планиметрии для 8–10 классов: трапеция, параллельные отрезки и площади

Задача 215505 • Сложность: 2 • 8-10 класс
Задача

Дана трапеция ABCD с основаниями  AD = a  и  BC = b.  Точки M и N лежат на сторонах AB и CD соответственно, причём отрезок MN параллелен основаниям трапеции. Диагональ AC пересекает этот отрезок в точке O. Найдите MN, если известно, что площади треугольников AMO и CNO равны.

Авторы:
Волчкевич М. А.
Разделы:
Планиметрия
Источники:
Московская математическая олимпиада Олимпиады и турниры 2010 год
Количество версий:
5
Решение
  Добавив к равновеликим треугольникамMOAиCON(см. рис.) треугольникAON, получим, что треугольникиAMNиACNтакже равновелики. Они имеют общее основаниеAN, а значит, точкиMиCравноудалены от прямойAN. А поскольку они, очевидно, лежат по одну сторону от этой прямой, прямыеMCиANпараллельны.   Имеем две пары подобных треугольниковMCNиAND(а значит,  AD:MN = AN:MC)  иMCBиANM(откуда  AN:MC = MN:BC).  Стало быть, AD:MN = MN:BC,  откуда  MN² =AD·BC = ab.
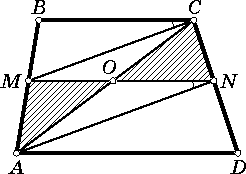
Ответ

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет