Олимпиадная задача про треугольники Саши и Пети – последовательности и делимость
Задача
Саша выложил треугольник со стороной из нескольких спичек, разделённый на маленькие треугольники (см. рис.), а Петя – такой же треугольник, сторона которого на три спички больше. Петя считает, что для этого ему потребовалось на 111 спичек больше чем Саше, а Саша с ним не согласен. Кто из мальчиков прав?
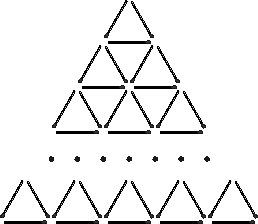
Решение
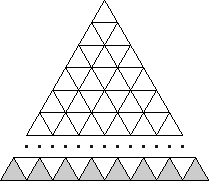
При увеличении длины стороны треугольника на одну спичку добавляется ряд маленьких треугольников снизу (см. рис.). Заметим, что в каждом следующем ряду на один маленький треугольник больше чем в предыдущем, значит, количество этих треугольников в трёх подряд идущих рядах выражается тремя последовательными натуральными числами. Следовательно, количество треугольников, добавленных Петей, является суммой трёх последовательных чисел, значит, делится на 3. Так как на каждый маленький треугольник расходуется ровно три спички, то количество спичек, добавленных Петей, должно быть кратно 9. Но 111 не делится на 9, следовательно, Петя ошибся.
Ответ
Прав Саша.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь