Олимпиадная задача по планиметрии: равнобедренность треугольника BMC
Задача
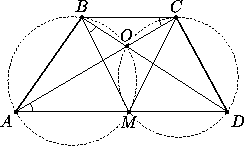
Диагонали трапеции ABCD пересекаются в точке O . Описанные окружности треугольников AOB и COD пересекаются в точке М на основании AD . Докажите, что треугольник BMC равнобедренный.
Решение
Первый способ.По теореме об углах, вписанных в окружность, 
OBM= OAM (см.
рис.). По определению трапеции OAM= OCB . Таким образом, OBM=
OCB . Аналогично доказывается, что OСM= OBC . Складывая полученные равенства, найдём,
что MBC= MCB , то есть, BM=CM .
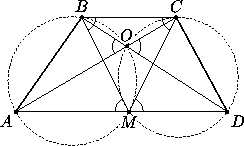
Второй способ.Рассмотрим цепочку равенств: CBM= BMA= BOA=
COD= CMD= BCM (см. рис.). Первое и пятое равенства вытекают из параллельности
оснований трапеции, второе и четвёртое
— из свойства вписанных углов, опирающихся на одну дугу, третье
— равенство вертикальных углов. Из доказанного вытекает, что CBM= BCM , то есть, BM=CM .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь