Олимпиадная задача по планиметрии: вписанный четырёхугольник и окружности (сложность 4/5)
Задача
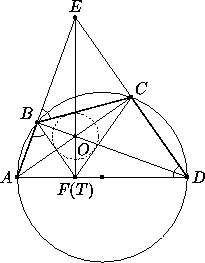
Четырёхугольник ABCD вписан в окружность с диаметром AD ; O — точка пересечения его диагоналей AC и BD является центром другой окружности, касающейся стороны BC . Из вершин B и С проведены касательные ко второй окружности, пересекающиеся в точке T . Докажите, что точка T лежит на отрезке AD .
Решение
Первый способ.Пусть
прямые АВ и CD пересекаются в точке Е (см. рис. 11.5а).
Заметим, что 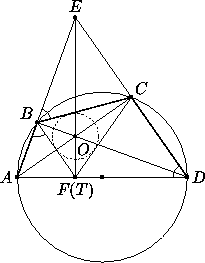 ACD =
ACD =  ABD = 90o (вписанные углы,
опирающиеся на диаметр). Тогда AC и BD — высоты треугольника DAE , а точка О является точкой пересечения высот этого
треугольника (ортоцентром). Следовательно, EF — еще
одна высота треугольника DAE — содержит точку О .
Докажем, что вторая окружность,
упомянутая в условии задачи, совпадает с окружностью, вписанной в
треугольник ВСF .
Воспользуемся вспомогательным
утверждением: высоты треугольника DAE являются биссектрисами
треугольника BCF (его ортотреугольника) ().
Следовательно, точка пересечения высот треугольника DAE (точка O ) является центром окружности, вписанной в треугольник BCF .
Тогда вписанная окружность совпадает с окружностью, заданной в
условии, поскольку эти окружности имеют общий центр и обе касаются
прямой ВС .
Таким образом, касательные к окружности, проведенные из точек В и С , являются сторонами треугольника BCF и пересекаются на
стороне AD в точке F , то есть точка F совпадает с точкой T . Следовательно, точка T лежит на диаметре AD , что и
требовалось.
() Для доказательства этого утверждения достаточно показать, что
ABD = 90o (вписанные углы,
опирающиеся на диаметр). Тогда AC и BD — высоты треугольника DAE , а точка О является точкой пересечения высот этого
треугольника (ортоцентром). Следовательно, EF — еще
одна высота треугольника DAE — содержит точку О .
Докажем, что вторая окружность,
упомянутая в условии задачи, совпадает с окружностью, вписанной в
треугольник ВСF .
Воспользуемся вспомогательным
утверждением: высоты треугольника DAE являются биссектрисами
треугольника BCF (его ортотреугольника) ().
Следовательно, точка пересечения высот треугольника DAE (точка O ) является центром окружности, вписанной в треугольник BCF .
Тогда вписанная окружность совпадает с окружностью, заданной в
условии, поскольку эти окружности имеют общий центр и обе касаются
прямой ВС .
Таким образом, касательные к окружности, проведенные из точек В и С , являются сторонами треугольника BCF и пересекаются на
стороне AD в точке F , то есть точка F совпадает с точкой T . Следовательно, точка T лежит на диаметре AD , что и
требовалось.
() Для доказательства этого утверждения достаточно показать, что  FBA
=
FBA
=  EBC (см. рис.11.5а). Это, в свою очередь, следует из
того, что каждый из этих углов равен углу ADE . Действительно,
EBC (см. рис.11.5а). Это, в свою очередь, следует из
того, что каждый из этих углов равен углу ADE . Действительно,  EBC =
90o -
EBC =
90o -  CBD = 90o -
CBD = 90o -  CAD =
CAD =  ADE . Аналогично, если рассмотреть
окружность, проходящую через точки B , F , D и E , получим,
что
ADE . Аналогично, если рассмотреть
окружность, проходящую через точки B , F , D и E , получим,
что  EBC =
EBC =  ADE .
Другой возможный способ —
доказать, что каждый из треугольников ABF и ВЕС подобен
треугольнику AED .
Второй способ.
ADE .
Другой возможный способ —
доказать, что каждый из треугольников ABF и ВЕС подобен
треугольнику AED .
Второй способ.
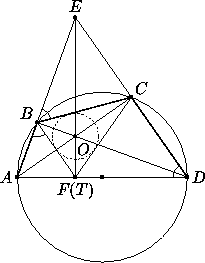
 ACK =
ACK =  BCA =
BCA =  BDA , следовательно,
около четырёхугольника OCDK можно описать окружность. При этом,
угол OCD — прямой (вписанный и опирается на диаметр AD ).
Значит, и угол OKD — также прямой.
Аналогично доказывается, что угол OPА — прямой.
Таким образом, через точку О проходят два перпендикуляра к одной прямой AD , что невозможно.
Значит, точки P и K совпадают с точкой T , что и требовалось.
При решении первым способом от учащихся не требуется
доказательство вспомогательного утверждения (если оно
сформулировано), а при решении вторым способом — не
требуется рассмотрения различных случаев расположения точки Т относительно прямой AD .
BDA , следовательно,
около четырёхугольника OCDK можно описать окружность. При этом,
угол OCD — прямой (вписанный и опирается на диаметр AD ).
Значит, и угол OKD — также прямой.
Аналогично доказывается, что угол OPА — прямой.
Таким образом, через точку О проходят два перпендикуляра к одной прямой AD , что невозможно.
Значит, точки P и K совпадают с точкой T , что и требовалось.
При решении первым способом от учащихся не требуется
доказательство вспомогательного утверждения (если оно
сформулировано), а при решении вторым способом — не
требуется рассмотрения различных случаев расположения точки Т относительно прямой AD .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь