Олимпиадная задача по математике: шашки на полоске, теория алгоритмов, 8-11 класс
Задача
Игровое поле представляет собой полоску1× N . В начале игры на нескольких крайних левых полях стоит по одной белой шашке, на стольких же крайних правых полях — по одной чёрной шашке. Белые и Чёрные ходят по очереди, начинают Белые. Ход заключается в передвижении одной из своих шашек в направлении противника (Белые ходят направо, Чёрные — налево). Можно делать простой ход или бить шашки соперника. При простом ходе разрешается перемещать шашку на любое число клеток, но нельзя перепрыгивать ни через свои шашки, ни через чужие. Бьют шашки соперника по тем же правилам, что и в обычных шашках: Шашка бьёт шашку соперника, стоящую на соседнем поле, если следующее за ним поле свободно. При этом своя шашка перемещается на это свободное поле, а побитая шашка соперника снимается с доски. Бить обязательно: если есть возможность бить, делать вместо этого простой ход какой-либо шашкой нельзя. Если шашка, побившая шашку соперника, может сразу побить следующую его шашку, она должна продолжать бить тем же ходом. Кто — Белые или Чёрные — победят в этой игре вне зависимости от игры партнёра? Рассмотрите случаи: а) У игроков по одной шашке, поле длиной N>2клеток; б) У игроков по две шашки, поле длиной N>4клеток; в) У игроков по три шашки, поле длиной N>6клеток; г)Дополнительное задание.Можно подумать, что численное преимущество решает исход игры. Придумайте и нарисуйте, однако, позицию, где у Белых меньше шашек, чем у Чёрных, и тем не менее, Белые начинают (с простого хода) и выигрывают.
Решение
В этой игре Белые, бесспорно, имеют преимущество, хотя иногда они и проигрывают. Клетки поля мы для удобства иногда будем нумеровать слева направо:1, 2, 3, .. (N-1), N . В пункте "а" приN=3Белые проиграют (этот тривиальный случай многие "прозевали"), а в остальных случаях — победят, передвинув шашку с клетки1на клетку(N-2). Эта атака — поставить свою шашку за одну клетку до шашки противника — будет часто в дальнейшем применяться Белыми. В пункте "б" Белые тоже, казалось бы, должны идти с клетки 2 на(N-3). Однако, такой ход возможен только еслиN-3>2, то естьN>5. В этом случае у Чёрных только один ход, следует размен, и возникает положение (рис. 5). Теперь Белые ходят с 1 на(N-4)(это возможно, так какN-4>1приN>5) и выигрывают.
Случай жеN=5разбирается отдельно. Все ходы там вынужденные,
и побеждают тоже Белые.
В пункте "в" Белые тоже побеждают, атакуя стандартным образом, но
это возможно только приN>8. Вот как пойдёт игра: Белые:3 
(N-4), размен и далее Белые повторяют атаку:2 (N-5). Оба эти хода возможны: приN>8заведомо
будет и N-4>3, и N-5>2. После второго хода Белых возникнет
ситуация как на рис 2. Теперь двигать левую чёрную шашку Чёрным
невыгодно, а второй шашкой они смогут сделать максимум 2 хода,
тогда как Белые(N-7)ходов. ПосколькуN-7 
2приN>8,
у Чёрных раньше кончатся ходы, и им придётся отдавать свою шашку на
съедение, что быстро приведёт их к проигрышу.
СлучаиN=7иN=8требуют отдельного разбора. ПриN=7ход у
Белых один, далее серия вынужденных разменов, и возникает позиция
(рис. 7), где Белые легко побеждают.
ПриN=8у Белых теоретически два возможных первых хода.
Поддаться первым ходом (3 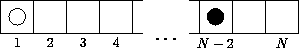5) оказывается
невыгодным: после серии вынужденных ходов имеем положение (рис. 8),
где ход Чёрных, так что они легко выигрывают, пойдя7 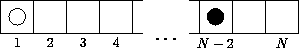5. Атаковать тоже не удаётся: после первого хода3 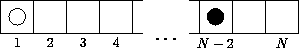4и разменов получается позиция (рис. 9). Ходить2 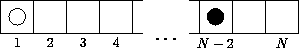4глупо, после же2 3следует8 7, Белые ходят1 2, Чёрные7 6, после чего Белые вынуждены пойти на клетку4и проиграть. Итак, приN=8победят Чёрные.
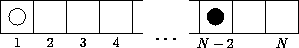
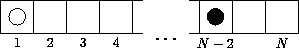
Возможное (видимо, простейшее) решение дополнительного задания представлено на рисунке 10. Пусть у Чёрных две шашки, у белых — только одна. Ходя на клетку влево, Белые вынуждают Чёрных сдать обе свои шашки следующим ходом.
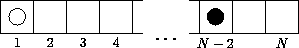
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь