Задание олимпиады: степень факториала простого p в факториале квадрата p – олимпиадная задача по теории чисел
Задача
Для каждого простого p найдите наибольшую натуральную степень числа p!, на которую делится число (p²)!.
Решение
Если (p²)! кратно (p!)n, то n ≤ p + 1, так как p входит в разложение числа p! на простые множители в степени 1 (а значит, в разложение числа (p!)n – в степени n), а в разложение числа (p²)! – в степени p + 1. Докажем, что (p²)! делится на (p!)p+1. Первый способ. Запишем p² различных элементов в виде таблицы p×p. Всего таких таблиц (p²)!. Две таблицы назовём эквивалентными, если одна получается из другой некоторыми перестановками элементов внутри строк,
а также некоторой перестановкой самих строк (всего p + 1 перестановка p объектов). В каждом классе эквивалентности (p!)p+1 таблиц. Поэтому (p²)! делится на (p!)p+1. Второй способ. 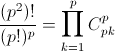 кратно p!, так как
кратно p!, так как 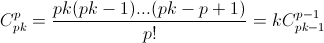 кратно k при всех k ≤ p.
Третий способ. Возьмём произвольное простое число q ≤ p и докажем, что в разложение числа (p!)p+1 на простые множители оно входит в степени, не большей, чем в разложение числа (p²)!.
кратно k при всех k ≤ p.
Третий способ. Возьмём произвольное простое число q ≤ p и докажем, что в разложение числа (p!)p+1 на простые множители оно входит в степени, не большей, чем в разложение числа (p²)!.
Пусть qn ≤ p < qn+1, тогда q2n ≤ p² < q2n+2. По формуле Лежандра (см. задачу 160553) достаточно проверить, что
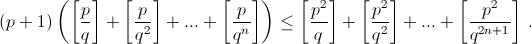
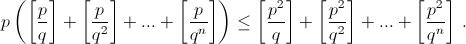 Кроме того,
Кроме того, 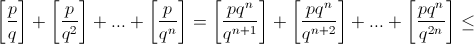
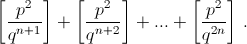
Ответ
p + 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь