Олимпиадная задача по планиметрии: прямые через центр вписанной окружности четырехугольника

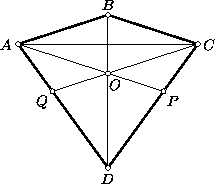
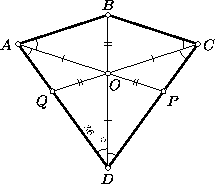
Пусть ABCD — данный четырёхугольник, O — центр вписанной в него окружности, прямые AO , CO — две из трёх прямых, данных в условии. а) Если точка O лежит на прямой AC , то эта прямая является осью симметрии четырёхугольника ABCD (т.к. лучи AO и CO являются биссектрисами углов A и C соответственно), поэтому прямые BO и DO одновременно обладают указанным свойством. Рассмотрим случай, когда прямые AO и CO не совпадают и пересекают границу четырёхугольника в точках P и Q соответственно (рис.), на котором для определённости P CD , Q AD ). Из условия следует, что треугольники AOQ и COP равновелики, а так как их высоты, опущенные из вершины O , равны, то AQ=CP . Кроме того, AOQ= COP , поэтому AO· OQ = CO· OP и, по теореме косинусов, 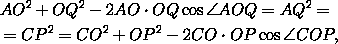откуда AO+OQ=CO+OP . Поэтому либо AO=OP и OQ=CO , либо AO=OC и OQ=OP (по теореме, обратной теореме Виета) и треугольники AOQ и COP равны. При этом, если AO=OP и OQ=CO , то OAQ = OPC , а значит AD|| CD , что неверно. Поэтому OAQ = OCP и AO=OC , откуда CAO= ACO , а значит, CAD= ACD и AD=CD , а тогда и AB=BC (т.к. AB+CD=BC+AD ). Значит, четырёхугольник ABCD симметричен относительно прямой BD , на которой, таким образом, лежит точка O , т.е. прямые BO и DO совпадают. б) В п. а) мы доказали, что четырёхугольник ABCD симметричен относительно одной из своих диагоналей. Если он симметричен относительно и другой диагонали, то он — ромб и его углы равны72^o, 108^o, 72^o, 108^o . Обратно, ромб с такими углами удовлетворяет условию задачи. Рассмотрим случай, когда ось симметрии только одна (без ограничения общности этот случай можно разбирать по рис.). Так же, как и в п. а), получаем, что треугольники AOB и DOP равновелики и равны. При этом OAB 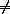OPD (иначе AB || CD и, в силу симметрии, BC || AD , а т.к. AC BD , то ABCD — ромб), так что OAB= ODP , откуда BAD= ADC = BCD < 90^o (т.к. AOD > 90^o , а значит, OAD <-2mu45^o ). Поэтому BAD= ADC = BCD=72^o , а ABC = 144^o . Четырёхугольник ABCD с такими углами, удовлетворяющий условию задачи, существует: его можно составить из равных треугольников AOB , COB , DOQ , DOP и равных треугольников AOQ , COP (рис.). Высоты первых четырёх треугольников, опущенные из вершины O , равны, поэтому точка O является центром окружности, вписанной в четырёхугольник ABCD ; каждая из прямых AO , BO , CO , DO делит его на два равносоставленных, а значит, и равновеликих многоугольника. Комментарий1. 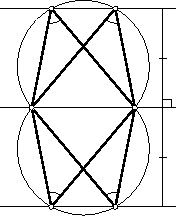Тот факт, что треугольник однозначно определяется одной из сторон, опущенной на неё высотой и противолежащим этой стороне углом, можно доказать чисто геометрически, используя следующее утверждение: геометрическим местом точек, из которых данный отрезок виден под данным углом, являются две дуги окружностей, стягиваемые этим отрезком как хордой, в которые данный угол вписан (рис.). 2. Четырёхугольник, для которого каждая из прямых, проходящих через вершину и центр вписанной окружности, делит его на две равновеликие части, — это либо ромб, либо выпуклый дельтоид, у которого три угла равны (не обязательно номеру текущей олимпиады в градусах!) и меньше четвёртого, т.е. углы которого имеют вид α, α, α, 360^o - 3α , причём α<360^o-3α < 180^o , или, что то же самое,60^o <α < 90^o .

б)72^o, 108^o, 72^o, 108^o или72^o, 72^o, 72^o, 144^o .