Олимпиадная задача: Касательная к графику y=sin(x) циркулем и линейкой. Планиметрия, 10-11 класс
Задача
На плоскости даны оси координат с одинаковым, но не обозначенным масштабом и график функции
y= sin x, x (0;α).
(0;α).
 (
(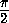 ;π);
б) α
;π);
б) α (0;
(0;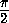 )?
)?
Решение
Касательная к графику функции y= sin x , где x (0; α),
проведённая в заданной его точке(x0, sin x0), имеет угловой
коэффициент, т.е. тангенс угла наклона к оси Ox , равный cos x0 ,
и для её построения при помощи циркуля и линейки достаточно построить
отрезок длины1. Действительно, имея отрезки1и sin x0 , можно
построить отрезок cos x0 (при помощи тригонометрического круга),
а значит, и угол, тангенс которого равен cos x0 . Покажем, как
построить отрезок длины 1 (т.е. восстановить
масштаб).
а) Из точки A=(a, sin a), где a
(0; α),
проведённая в заданной его точке(x0, sin x0), имеет угловой
коэффициент, т.е. тангенс угла наклона к оси Ox , равный cos x0 ,
и для её построения при помощи циркуля и линейки достаточно построить
отрезок длины1. Действительно, имея отрезки1и sin x0 , можно
построить отрезок cos x0 (при помощи тригонометрического круга),
а значит, и угол, тангенс которого равен cos x0 . Покажем, как
построить отрезок длины 1 (т.е. восстановить
масштаб).
а) Из точки A=(a, sin a), где a (
(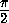 ,α), лежащей на графике функции,
опустим перпендикуляр на ось Oy (рис. 11-3-sol-1).
Так как sin(π-a)= sin a , то
этот перпендикуляр пересечёт график функции y= sin x в точке B=(π-a, sin a). Через середину отрезка AB проведём прямую,
перпендикулярную оси Ox . Она пересечёт график в точке(
,α), лежащей на графике функции,
опустим перпендикуляр на ось Oy (рис. 11-3-sol-1).
Так как sin(π-a)= sin a , то
этот перпендикуляр пересечёт график функции y= sin x в точке B=(π-a, sin a). Через середину отрезка AB проведём прямую,
перпендикулярную оси Ox . Она пересечёт график в точке(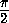 ,1). Отрезок этой прямой от оси Ox до
графика функции y= sin x имеет длину 1.
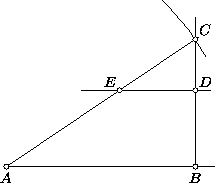
б) Здесь несколько труднее построить
отрезок единичной длины. Остальные построения будут такими же.
Пусть a и b произвольные точки на оси Ox , удовлетворяющие
условию0<b<a<α . Построим отрезок AB длины sin a+ sin
b . Через точку B проведём луч l , перпендикулярный отрезку AB . Окружность с центром в точке A и радиусом2 sin
,1). Отрезок этой прямой от оси Ox до
графика функции y= sin x имеет длину 1.
б) Здесь несколько труднее построить
отрезок единичной длины. Остальные построения будут такими же.
Пусть a и b произвольные точки на оси Ox , удовлетворяющие
условию0<b<a<α . Построим отрезок AB длины sin a+ sin
b . Через точку B проведём луч l , перпендикулярный отрезку AB . Окружность с центром в точке A и радиусом2 sin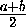 пересекает луч l в точке C (рис. 11-3-sol-2). Так как sin
a+ sin b=2 sin
пересекает луч l в точке C (рис. 11-3-sol-2). Так как sin
a+ sin b=2 sin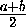 cos
cos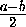 , то
, то  CAB=
CAB=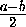 . На отрезке BC отметим точку D такую, что BD= sin
. На отрезке BC отметим точку D такую, что BD= sin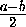 . Через точку D проведём прямую, параллельную
отрезку AB . Эта прямая пересечёт отрезок AC в точке E . Длина
отрезка AE равна 1, так как
. Через точку D проведём прямую, параллельную
отрезку AB . Эта прямая пересечёт отрезок AC в точке E . Длина
отрезка AE равна 1, так как
sin CAB= sin
CAB= sin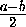 =
=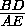 .
.
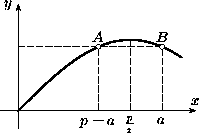
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь