Олимпиадная задача Сергеевa И. Н. по производной для 10-11 классов: уровень воды в бассейне
Задача
Когда из бассейна сливают воду, уровень h воды в нём меняется в зависимости от времени t по закону
h(t)=at2+bt+c,
Решение
Так как h'(t0)=0и h(t0)=0, то a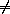 0(в противном случае
функция h была бы нулевой, и уровень воды в бассейне, вопреки
условию задачи, не мог бы понизиться), а абсцисса и ордината вершины
параболы y=h(t)равны соответственно t0 и 0, поэтому
0(в противном случае
функция h была бы нулевой, и уровень воды в бассейне, вопреки
условию задачи, не мог бы понизиться), а абсцисса и ордината вершины
параболы y=h(t)равны соответственно t0 и 0, поэтому
h(t)=a(t-t0)2, t t0.
t0.
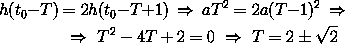 и, учитывая, что T>1, окончательно получаем T=2+
и, учитывая, что T>1, окончательно получаем T=2+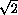 .
Комментарий.Из законов физики известно, что функция y=h(t)удовлетворяет дифференциальному уравнению
.
Комментарий.Из законов физики известно, что функция y=h(t)удовлетворяет дифференциальному уравнению
y'=-k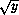 , k>0,
, k>0,
Ответ
2+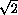 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет