Олимпиадная задача по планиметрии и инвариантам о бусинках на кольце, 8-10 класс

  Пусть при каком-то начальном расположении бусинок нашлась последовательность ходов, в результате которой какая-то бусинка прошла полный круг против часовой стрелки или больше. Обозначим начальное положение этой бусинки O. Тогда положения бусинок определяются углом от точки O с точностью до 2π, причём углы по часовой стрелке будем считать со знаком минус, а углы против часовой стрелки со знаком плюс. Занумеруем бусинки по порядку. Обозначим через α_i угол до i-й бусинки. Тогда вначале  – 2π < α₁ < α₂ < ... < α₂₀₀₉ = 0  (см. рис.).

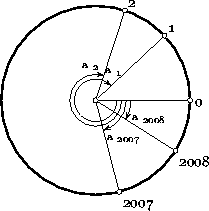
  Заметим, что перемещениюi-й бусинки соответствует замена α_iна  ½ (α_i–1+ α_i+1)  при  i= 2, ..., 2008,  на  ½ (α₂+ α₂₀₀₉– 2π)  при  i= 1,  на ½ (α₁+ α₂₀₀₈+ 2π)  при  i= 2009.  То, что бусинкаOпрошла полный круг или более, означает, что угол α₂₀₀₉стал не меньше 2π. Но вначале α_i<^2πi/₂₀₀₉,  и при вышеуказанных преобразованиях это свойство сохраняется. Значит, α₂₀₀₉всегда меньше 2π. Противоречие.

Не существуют.