Олимпиадная задача — Петя и Вася: определение подъезда по плану домов
Задача
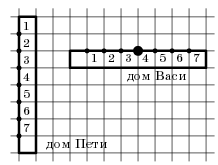
Петя и Вася живут в соседних домах (см. план на рисунке). Вася живет в четвёртом подъезде. Известно, что Пете, чтобы добежать до Васи кратчайшим путем (не обязательно идущим по сторонам клеток), безразлично, с какой стороны обегать свой дом. Определите, в каком подъезде живет Петя.
Решение
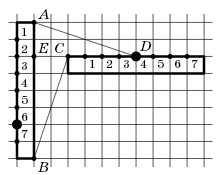
Кратчайший путь от точки A до Васиного подъезда – отрезок AD (см. рис.). Кратчайший путь от точки B до Васиного подъезда – это путь по отрезку BC, а далее – по отрезку CD. Так как треугольники AED и CEB равны, AD = BC. Поэтому пути от точек A и B до Васиного подъезда отличаются на 4 клетки.
Ответ
В шестом подъезде.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет