Назад

Олимпиадная задача по планиметрии: пересечения в ромбе, 8-9 класс

Задача 211852 • Сложность: 2 • 8-9 класс
Задача

На стороне BC ромба ABCD выбрана точка M. Прямые, проведённые через M перпендикулярно диагоналям BD и AC, пересекают прямую AD в точках P и Q соответственно. Оказалось, что прямые PB, QC и AM пересекаются в одной точке. Чему может быть равно отношение  BM : MC?

Авторы:
Акопян А. В. Берлов С. Л. Петров Ф.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2006-2007 Заключительный этап
Количество версий:
5
Решение
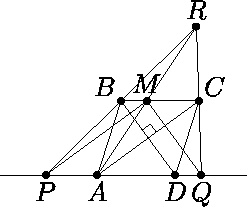
Обозначим черезRточку пересеченияPB, QCиAM(см. рис.). Заметим, что  PM || AC,  MQ || BD,  поэтому четырёхугольникиPMCAиQMBD– параллелограммы. Значит,  MC = PA,  BM = DQ  и  PQ = PA + AD + DQ = MC + AD + BM= 2BC.  Так как  BC || PQ  и  BC= ½PQ,  тоBC– средняя линия треугольникаPRQ. Значит, иBM– средняя линия треугольникаARP. Тогда  MC = PA= 2BM.
Ответ

1 : 2.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет