Олимпиадная задача по планиметрии для 9-10 классов: окружности и середины в треугольнике
Задача
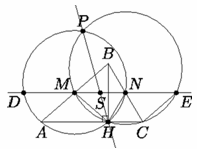
Дан остроугольный треугольник ABC. Точки M и N – середины сторон AB и BC соответственно, точка H – основание высоты, опущенной из вершины B. Описанные окружности треугольников AHN и CHM пересекаются в точке P (P ≠ H). Докажите, что прямая PH проходит через середину отрезка MN.
Решение
Пусть прямая MN вторично пересекает описанные окружности Ω1 и Ω2 треугольников AHN и CHM в точках D и E, а прямую PH – в точке S. Поскольку HN– медиана прямоугольного треугольника BHC, то HN = CN и ∠NHC = ∠NCH. Из параллельности хорд ME и HC окружности Ω2 следует, что четырёхугольник MHCE – равнобокая трапеция, поэтому HM = CE и ∠MHC = ∠ECH. Следовательно,
∠MHN = ∠MHC – ∠NHC = ∠ECH – ∠NCH = ∠ECN. Значит, треугольники MHN и ECN равны по двум сторонам и углу между ними, откуда
NE = MN. Аналогично DM = MN. Обозначим длину этих трёх отрезков через a, а длины отрезков MS и NS через x и y. Из вписанности четырёхугольников DHNP и MHEP получаем MS·SE = PS·SH = NS·SD, то есть x(a + y) = y(a + x), или ax = ay. Таким образом, S – середина MN, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь