Олимпиадная задача по планиметрии для 9–11 класса от Агахановa Н. Х.: длинные векторы и их сумма
Задача
Дан набор из n>2векторов. Назовем вектор набора длинным, если его длина не меньше длины суммы остальных векторов набора. Докажите, что если каждый вектор набора– длинный, то сумма всех векторов набора равна нулю.
Решение
Первое решение.Пусть сумма 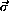 всех векторов отлична от нуля ( |
всех векторов отлична от нуля ( |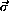 |=s>0). Введем прямоугольную систему координат Oxy , в которой ось Ox сонаправлена с
|=s>0). Введем прямоугольную систему координат Oxy , в которой ось Ox сонаправлена с 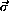 . Пусть
. Пусть 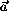 – длинный вектор набора, т.е. он не короче, чем
– длинный вектор набора, т.е. он не короче, чем 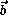 =
=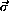 -
-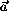 . Поскольку y -координаты векторов
. Поскольку y -координаты векторов 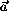 и
и 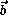 равны по модулю, то x -координата ax вектора
равны по модулю, то x -координата ax вектора 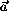 по модулю не меньше, чем x -координата bx=s-ax вектора
по модулю не меньше, чем x -координата bx=s-ax вектора 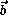 . Отсюда получаем, что ax
. Отсюда получаем, что ax s/2. Теперь, если все векторы набора длинные, то сумма их x -координат не меньше ns/2>s , но эта сумма
равна s . Противоречие.
Второе решение.Обозначим данные векторы через ak ( k=1,..,n ), а их сумму через
s/2. Теперь, если все векторы набора длинные, то сумма их x -координат не меньше ns/2>s , но эта сумма
равна s . Противоречие.
Второе решение.Обозначим данные векторы через ak ( k=1,..,n ), а их сумму через 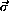 .
По условию |
.
По условию |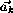 |
|  |
|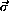 -
- 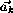 | . Возведем это неравенство в квадрат:
| . Возведем это неравенство в квадрат: 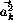

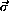 2 - 2
2 - 2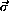 ·
·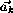 +
+ 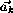 2 . Просуммировав такие неравенства по всем k от 1 до n , получаем0
2 . Просуммировав такие неравенства по всем k от 1 до n , получаем0 n
n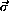 2 - 2
2 - 2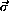 ·(
·(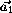 +
+ 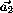 + ..+
+ ..+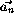 ), т.е.0
), т.е.0 (n-2)
(n-2) 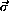 2 . Значит,
2 . Значит, 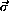 =
=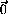 .
.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь