Олимпиадная задача по планиметрии для 8–9 классов о вписанном четырёхугольнике
Задача
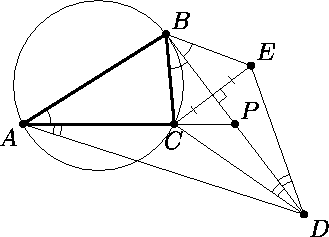
Дан треугольник ABC, в котором AB > BC. Касательная к его описанной окружности в точке B пересекает прямую AC в точке P. Точка D симметрична точке B относительно точки P, а точка E симметрична точке C относительно прямой BP. Докажите, что четырёхугольник ABED – вписанный.
Решение
Так как PB – касательная, то ∠BAC = ∠PBC. Следовательно, треугольники PBC и PAB подобны по двум углам, и PB : PC = PA : PB. Значит,
PD : PC = PA : PD. Следовательно, треугольники PDC и PAD подобны, и ∠PDC = ∠PAD. Так как точки E и C симметричны относительно BD, то
∠BED = ∠BCD = 180° – ∠CBD – ∠CDB = 180° – ∠CAB – ∠CAD = 180° – ∠BAD, то есть ∠BAD + ∠BED = 180°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет