Олимпиадная задача по планиметрии: треугольники и выпуклый шестиугольник

  Достаточно доказать, что  Q₂Q₆ = Q₅Q₃,  Q₂Q₄ = Q₅Q₁  и  Q₄Q₆ = Q₁Q₃.  Докажем одно из этих равенств, остальные доказываются аналогично.   Первый способ. Обозначим углы шестиугольника при вершинах P₁, ..., P₆ через α₁, ..., α₆; тогда  α₁ + ... + α₆ = 720°.  Рассмотрим четырёхугольник P₂P₃P₄Q₃. Все его стороны равны, поэтому он является ромбом. Аналогично ромбом является четырёхугольник P₄P₅P₆Q₅. Поэтому

∠P₃P₄Q₃ = 180° – ∠P₂P₃P₄ = 180° – α₃  и  ∠P₅P₄Q₅ = 180° – α₅.  Значит,  ∠Q₃P₄Q₅ = |∠P₃P₄P₅ – ∠P₃P₄Q₃ – ∠P₅P₄Q₅| = |α₃ + α₄ + α₅ – 360°|.  Аналогично ∠Q₂P₁Q₆ = |α₆ + α₁ + α₂ – 360°| = |(720° – α₃ – α₄ – α₅) – 360°| = ∠Q₃P₄Q₅.  Следовательно, треугольники Q₂P₁Q₆ и Q₃P₄Q₅ равны по двум сторонам  (Q₂P₁ = P₁Q₆ = Q₃P₄ = P₄Q₅)  и углу между ними, откуда  Q₂Q₆ = Q₅Q₃.   Второй способ. Как и выше, заметим, что четырёхугольники P₃P₄P₅Q₄ и P₄P₅P₆Q₅ – ромбы. Значит, 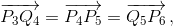    четырёхугольник P₃Q₄P₆Q₅ – параллелограмм, и середины отрезков P₃P₆ и Q₄Q₅ совпадают. Аналогично совпадают середины отрезков P₃P₆ и Q₁Q₂. Следовательно, отрезки Q₁Q₂ и Q₄Q₅ имеют общую середину (совпадающую с серединой P₃P₆), четырёхугольник Q₄Q₂Q₅Q₁ – параллелограмм, и  Q₅Q₁ = Q₂Q₄.

Ответ задачи отсутствует