Олимпиадная задача: бесконечная арифметическая прогрессия в числовой последовательности (Мурашкин М. В., 9–11 класс)
Задача
Последовательность(an)задана условиями a1= 1000000, an+1=n[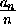 ]+n . Докажите, что в ней можно выделить бесконечную подпоследовательность, являющуюся арифметической прогрессией.
]+n . Докажите, что в ней можно выделить бесконечную подпоследовательность, являющуюся арифметической прогрессией.
Решение
Заметим, что числа kn=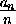 =[an n]+1– натуральные, причем
=[an n]+1– натуральные, причем
kn+1=[an+1 n+1]+1=[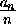 ]+1
=kn+[-
]+1
=kn+[-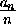 ]+1
]+1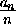 kn-1+1=kn.
kn-1+1=kn.
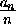 n выполняется равенство ad+2-ad+1=(d+1)kd+1-dkd=(d+1)k-dk=k , то есть вся подпоследовательность an+1,an+2,an+3,.. является арифметической прогрессией с разностью k .
n выполняется равенство ad+2-ad+1=(d+1)kd+1-dkd=(d+1)k-dk=k , то есть вся подпоследовательность an+1,an+2,an+3,.. является арифметической прогрессией с разностью k .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет