Олимпиадная задача по стереометрии: пересечение сфер и свойства точек, 10–11 класс
Задача
В пространстве даны две пересекающиеся сферы разных радиусов и точка A, принадлежащая обеим сферам. Докажите, что в пространстве существует точка B, обладающая следующим свойством: если через точки A и B провести произвольную окружность, то точки ее повторного пересечения с данными сферами будут равноудалены от B.
Решение
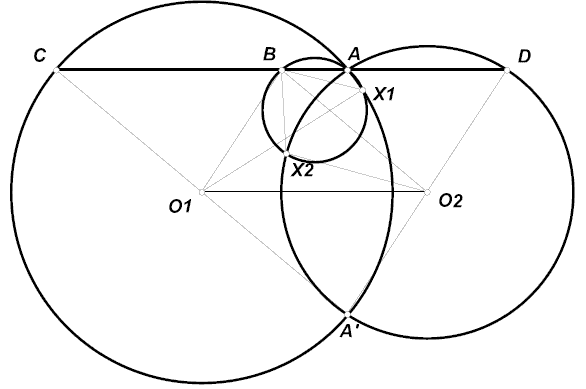
Проведём через A прямую, параллельную линии центров данных сфер, и найдём вторые точки C, D ее пересечения со сферами. Покажем, что середина B отрезка CD – искомая точка. Возьмем произвольную окружность, проходящую через A и B, и рассмотрим сечения сфер плоскостью этой окружности. Эти сечения представляют собой две окружности, одна из которых проходит через точки A и C, другая – через A и D. Центрами этих окружностей будут проекции O1, O2 центров сфер на плоскость сечения, следовательно, прямые O1O2 и CD параллельны. Поэтому достаточно доказать плоский аналог утверждения задачи.
Пусть X1, X2 – вторые точки пересечения окружности, проходящей через A и B, с данными окружностями; A' – вторая точка пересечения данных окружностей. Тогда O1O2 – средняя линия треугольника A'CD, то есть CB = BD = O1O2. Следовательно, O1B = O2D = O2X2, O2B = O1C = O1C1. Кроме того, центр O окружности ABX1X2O1 и O2, поэтому
∠BO1X1 = ∠BO1O + ∠OO1X1 = ∠BO1O + ∠AO1O = ∠AO2O + ∠BO2O = ∠BO2O + ∠OO2X2 = ∠BO2X2. Таким образом, треугольники O1X1B и O2BX2 равны, а значит, BX1 = BX2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь