Назад

Олимпиадная задача по планиметрии для 8–9 классов: окружности в параллелограмме

Задача 211724 • Сложность: 3 • 8-9 класс
Задача

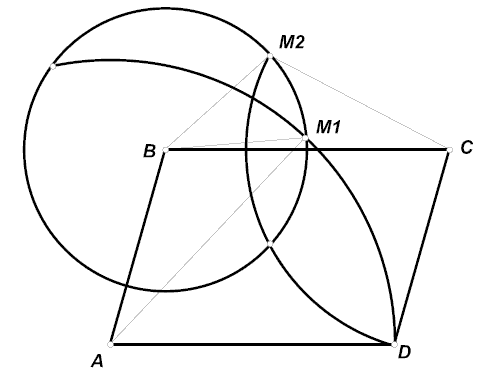
Дан параллелограмм ABCD, в котором  AB = a,  AD = b.  Первая окружность имеет центр в вершине A и проходит через D, вторая имеет центр в C и проходит через D. Произвольная окружность с центром B пересекает первую окружность в точках M1, N1, а вторую – в точках M2, N2. Чему равно отношение  M1N1 : M2N2?

Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина Заочный тур IV Олимпиада по геометрии имени И.Ф. Шарыгина (2008 г.)
Количество версий:
4
Решение

ТочкиM1,N1симметричны относительно прямойAB, так чтоM1N1равно удвоенному расстоянию отM1доAB. АналогичноM2N2равно удвоенному расстоянию отM2доBC. Кроме того,  CM2=CD = AB,  AM1=AD = BC,  BM1=BM2,  и значит, треугольникиABM1иCM2Bравны. Поэтому искомое отношение, равное отношению высот этих треугольников, обратно отношению соответствующих сторон, то есть равно  b:a.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет