Олимпиадная задача по планиметрии: неравенство для треугольника, сложность 4, 9–10 класс
Задача
Докажите, что для треугольника со сторонами a , b , c и площадью S выполнено неравенство
a2+b2+c2-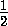
(|a-b|+|b-c|+|c-a|)2
4
S.
Решение
Первое решение. Пусть C — средний угол треугольника. Тогда |b-c|+|c-a|=|a-b| и левая часть неравенства равна
a2+b2+c2-2(a-b)2=4ab-(a2+b2-c2)=2ab(2- cos C).
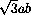sin C , данное неравенство
равносильно следующему
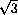sin C.
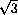sin C=2 cos(C-
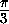), следовательно, данное
неравенство всегда справедливо и обращается в равенство только при C=60o .
Второе решение. Вновь полагая, что c — средняя сторона треугольника, обозначим x=p-a , y=p-b , z=p-c , где p — полупериметр, и запишем левую часть в виде
a2+b2-(a-b)2+c2-(a-b)2=2ab+4xy=2(x+z)(y+z)+4xy=2pz+6xy.
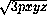, неравенство принимает вид
pz+3xy-2=(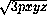
-
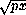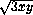)2 0.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет