Олимпиадная задача по планиметрии: Найдите центр вписанной окружности треугольника
Задача
Дан треугольник ABC и линейка, на которой отмечены два отрезка, равные AC и BC . Пользуясь только этой линейкой, найдите центр вписанной окружности треугольника, образованного средними линиями ABC .
Решение
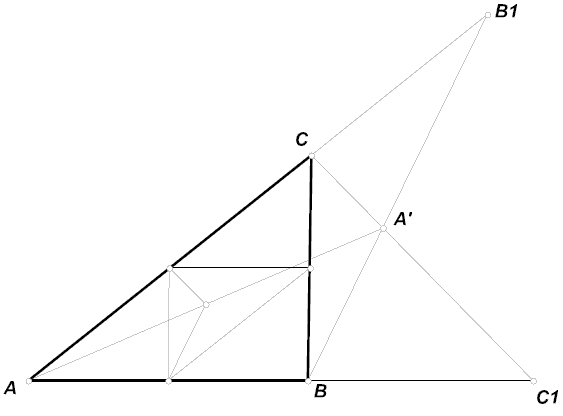
Отложим на продолжении стороны AB за точку B и на продолжении стороны AC за точку C отрезки BC1=CB1=BC . Пусть A' — точка пересечения BB1 и CC1 . Тогда прямая AA' проходит через искомую точку.
Действительно, так как треугольники BCB1 и CBC1 равнобедренные, прямые BB1 и CC1 параллельны биссектрисам углов C и B . Поэтому при гомотетии с центром A и коэффициентом1/2эти прямые перейдут в биссектрисы углов серединного треугольника, а точка A' — в искомый центр.
Аналогично, используя второй отмеченный на линейке отрезок, построим прямую, проходящую через B и исходную точку.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь