Олимпиадная задача по планиметрии: прямая, высоты и биссектриса в треугольнике
Задача
Прямая, соединяющая центр описанной окружности и точку пересечения высот неравнобедренного треугольника, параллельна биссектрисе одного из его углов. Чему равен этот угол?
Решение
Пусть O — центр описанной окружности треугольника ABC, H — его
ортоцентр, и прямая OH параллельна биссектрисе угла C . Так как эта
биссектриса пересекает описанную окружность в середине C' дуги AB , OC'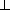 
AB , т.е.
четырехугольник OC'CH — параллелограмм и CH = OC' = R . С другой стороны, CH = 2R | cos C| , значит угол C равен60o или120o . Но в первом случае лучи CO и CH симметричны относительно биссектрисы угла C , так что прямая OH не может
быть параллельна этой биссектрисе. Следовательно, C = 120o .
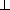
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь