Олимпиадная задача по планиметрии: Параллельность прямых в треугольнике, 8-10 класс
Задача
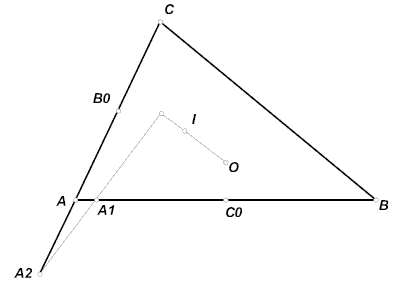
Имеется треугольник ABC. На луче BA отложим точку A1, так что отрезок BA1 равен BC. На луче CA отложим точку A2, так что отрезок C2 равен BC. Аналогично построим точки B1, B2 и C1, C2. Докажите, что прямые A1A2, B1B 2, C1C2 параллельны.
Решение
Пусть O, I – центры описанной и вписанной окружностей треугольника. Так как BI – биссектриса угла B равнобедренного треугольника A1BC,
A1I = IC. Аналогично A2I = IB. Следовательно, A1I² – A2I² = IC² – IB² = (p – c)² – (p – b)² = a(b – c). С другой стороны, если B0, C0 – середины AC и AB, то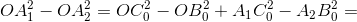 
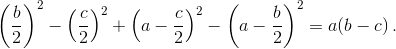Следовательно, прямые A1A2 и OI перпендикулярны (см. задачу 153602). Аналогично получаем, что прямая OI перпендикулярна двум другим прямым.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь