Олимпиадная задача по планиметрии для 9–10 классов про симметрии диагоналей четырёхугольника
Задача
Прямые, симметричные диагонали BD четырёхугольника ABCD относительно биссектрис углов B и D, проходят через середину диагонали AC.
Докажите, что прямые, симметричные диагонали AC относительно биссектрис углов A и C, проходят через середину диагонали BD.
Решение
Пусть P – середина AC, L – точка пересечения диагоналей. Применив теорему синусов к треугольникам ABP, ABL, CBP, CBL, получаем, что
AL/CL = (AB/CB)². Аналогично AL/CL = (AD/CD)², то есть BC : CD = AB : AD = sin∠BDA : sin∠DBA = sin∠CDP : sin∠CBP. Следовательно, прямые BP и CP симметричны относительно AC.
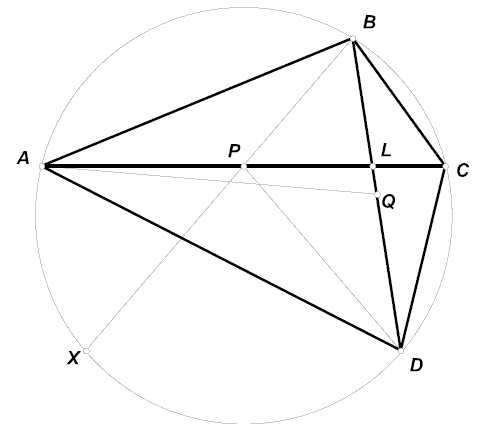
Пусть X – вторая точка пересечения прямой BP с описанной окружностью треугольника ABC. Точка, симметричная X относительно серединного перпендикуляра к AC лежит как на PD, так и на BD, и, значит, совпадает с D. Таким образом, четырёхугольник ABCD – вписанный, и по теореме Птолемея (см. задачу 152468) AB·CD = AD·BC = ½ AC·BD.
Пусть прямая, симметричная AC относительно биссектрисы угла A, пересекает BD в точке Q. Тогда треугольники ABQ и ACD подобны, следовательно, AB : AC = BQ : BD и BQ = ½ BD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь