Задачи Подборки Авторы

Олимпиадная задача по планиметрии: построение квадрата по вершине и расстояниям

Задача 211710 • Сложность: 3 • 8-9 класс

Задача

Постройте квадрат ABCD , если даны его вершина A и расстояния от вершин B и D до фиксированной точки плоскости O .

Решение

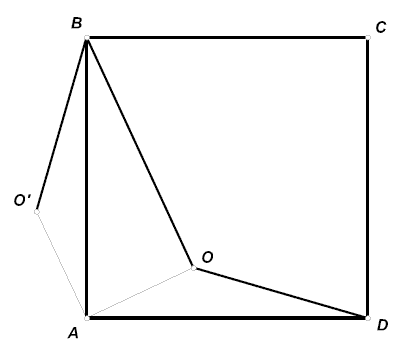
Пусть O' — такая точка, что AO=AO' и OAO'=90^o . Тогда O'AB= OAD и, так как AB=AD , треугольники OAD и O'AB равны. Следовательно, O'B=OD и, зная длины отрезков OB , O'B , можно построить точку B , а затем и весь квадрат. Задача имеет два решения, симметричных относительно прямой OA .