Олимпиадная задача по планиметрии: центры внешних треугольников и медианы
Задача
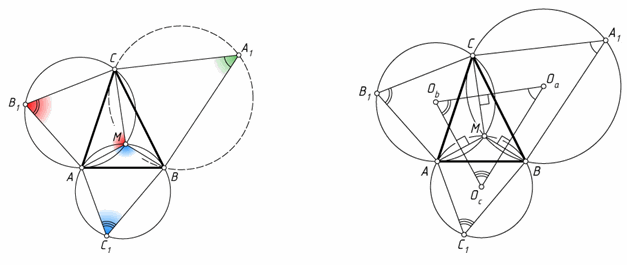
На сторонах треугольника ABC внешним образом построены правильные треугольники.
Докажите, что их центры образуют правильный треугольник, причём его центр совпадает с точкой пересечения медиан треугольника ABC.
Решение
Заметим, что если через точку T, лежащую на стороне YZ равностороннего треугольника XYZ с центром O и делящую это сторону в отношении
YT : TZ = 1 : 2, провести прямую, параллельную стороне XY (рис. слева), то эта прямая пройдёт через точку O и ∠ZOT = 90°. Отметим на сторонах AB и AC данного треугольника ABC такие точки K и L, что BK : AK = 1 : 2 и CL : AL = 1 : 2 (рис. справа). Тогда KL || BC, а середина M отрезка KL – точка пересечения медиан треугольника ABC. Построим внешним образом на сторонах AK и AL треугольника AKL как на гипотенузах прямоугольные треугольники AC1K и AB1L с углами 60° при вершинах K и L. Тогда точки C1 и B1 – центры правильных треугольников, о которых говорится в условии задачи. Согласно задаче 211667 MC1 = MB1 и ∠B1MC1 = 2∠ALB1 = 120°. Если A1 – центр равностороннего треугольника, построенного внешним образом на стороне BC, то аналогично MA1 = MB1 и ∠A1MB1 = 120°. Следовательно, A1B1C1 – равносторонний треугольник, а M – его центр.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь