Олимпиадная задача по стереометрии: двугранный угол в усечённой пирамиде с ромбом ABCD
Задача
Нижним основанием четырёхугольной усечённой пирамиды является ромб ABCD , у которого AB=4и  BAD=60o . AA1, BB1, CC1, DD1– боковые рёбра усечённой пирамиды, ребро A1B1=2, ребро CC1перпендикулярно плоскости основания и равно
2. На ребре BC взята точка M так, что BM=3, и через точки B1, M и центр ромба ABCD проведена плоскость. Найдите двугранный угол
между этой плоскостью и плоскостью AA1C1C .
BAD=60o . AA1, BB1, CC1, DD1– боковые рёбра усечённой пирамиды, ребро A1B1=2, ребро CC1перпендикулярно плоскости основания и равно
2. На ребре BC взята точка M так, что BM=3, и через точки B1, M и центр ромба ABCD проведена плоскость. Найдите двугранный угол
между этой плоскостью и плоскостью AA1C1C .
Решение
Пусть O – центр ромба ABCD . Из треугольника OMB находим, что
OM =  =
=
 =
=  .
.
Построим линейный угол двугранного угла между этими плоскостями. Для этого
из точки C1опустим перпендикуляр C1K на ребро OE этого
двугранного угла, а из точки K восставим перпендикуляр к OE в плоскости B1MO . Пусть этот перпендикуляр пересекается с прямой B1E в точке L . Тогда C1KL – искомый линейный угол угол. Обозначим  C1KL=γ . Для его нахождения вычислим все стороны треугольника C1KL .
C1KL=γ . Для его нахождения вычислим все стороны треугольника C1KL .
Поскольку MC = 1 =  B1C1и MC || B1C1, отрезок MC – средняя линия треугольника B1C1E , поэтому C – середина
отрезка EC1, а т.к. OC
B1C1и MC || B1C1, отрезок MC – средняя линия треугольника B1C1E , поэтому C – середина
отрезка EC1, а т.к. OC  EC1, то медиана OC треугольника EOC1является его высотой. Значит, треугольник EOC1– равнобедренный. Кроме
того, из прямоугольного треугольника COC1находим, что
EC1, то медиана OC треугольника EOC1является его высотой. Значит, треугольник EOC1– равнобедренный. Кроме
того, из прямоугольного треугольника COC1находим, что
OC1= =
= 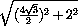 =
=
 = 4 = EC1,
= 4 = EC1,
 = 2
= 2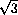 .
.
В треугольнике OME известно, что
ME = 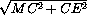 =
=  =
= , OE=4, OM=
, OE=4, OM= .
.
 OEM=ϕ . Тогда
OEM=ϕ . Тогда
cos ϕ = 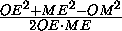 =
=
 =
=  ,
tg ϕ =
,
tg ϕ = 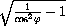 =
= 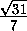 .
.
KL = KE tg ϕ =  OE tg ϕ = 2·
OE tg ϕ = 2· 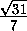 =
=
 ,
LE =
,
LE =  =
=  =
=  .
.
 B1EC1 = β . Тогда
B1EC1 = β . Тогда
tg β =  =
=  ,
cos β =
,
cos β =  =
=  .
.
LC1 =  =
=  .
.
cos γ =  =
=
 =
=
 .
.
Ответ
arccos  = arctg
= arctg  .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь