Олимпиадная задача по планиметрии и стереометрии: тетраэдр, сфера и точки на рёбрах для 10-11 класса
Задача
Ребро правильного тетраэдра ABCD равно a . На рёбрах AB и CD взяты точки E и F так, что описанная около тетраэдра сфера пересекает прямую, проходящую через E и F , в точках M и N . Найдите длину отрезка EF , если ME:EF:FN=3:12:4.
Решение
Положим ME = 3t , EF=12t , FN=4t . Пусть P и Q – середины рёбер AB и CD соответственно. Отрезок, соединяющий середины противоположных
рёбер правильного тетраэдра, перпендикулярен этим рёбрам, его длина
равна 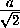 , где a – длина ребра тетраэдра.
, где a – длина ребра тетраэдра.
Обозначим PE = x , FQ=y . По теореме о произведении отрезков пересекающихся хорд шара AE· EB = ME· EN , CF· FD = NF· FM , или
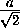 -x)(
-x)(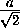 +x)=3t· 16t,
(
+x)=3t· 16t,
(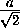 -y)(
-y)(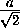 +y)=4t· 15t.
+y)=4t· 15t.
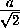 -x2 = 48t2,
-x2 = 48t2, 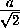 -y2 = 60t2,
-y2 = 60t2,
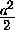 -108t2.
-108t2.
Из прямоугольных треугольников EPQ и FQP находим, что
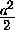 + y2.
+ y2.
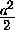 -108t2 +
-108t2 + 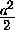 , откуда t2 =
, откуда t2 =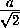 , t =
, t = 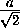 . Следовательно, EF = 12t =
. Следовательно, EF = 12t = 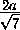 .
.
Ответ
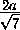 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет