Олимпиадная задача по стереометрии: сечение правильной четырёхугольной пирамиды
Задача
В правильной четырёхугольной пирамиде SABCD с вершиной S сторона
основания пирамиды равна b , а высота пирамиды равна b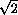 . Шар,
вписанный в эту пирамиду, касается боковой грани SAD в точке K .
Найдите площадь сечения пирамиды, проходящего через ребро AB и точку K .
. Шар,
вписанный в эту пирамиду, касается боковой грани SAD в точке K .
Найдите площадь сечения пирамиды, проходящего через ребро AB и точку K .
Решение
Пусть SH – высота данной пирамиды, SM – апофема, лежащая в грани ASD . Тогда точка K касания шара с плоскостью этой грани лежит на отрезке SM , MK = MH = 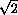 как отрезки касательных, проведённых к сфере из
одной точки. Из прямоугольного треугольника SMH находим, что
как отрезки касательных, проведённых к сфере из
одной точки. Из прямоугольного треугольника SMH находим, что
SM = 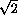 =
= 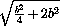 =
= 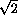 b.
b.
SK = SM-MK = 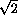 b-
b-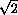 =b,
=b, 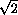 = 2,
= 2,
Секущая плоскость проходит через прямую AB , параллельную плоскости CSD , и
пересекает эту плоскость по прямой PQ (точка Q на ребре SC ), поэтому
сечение APQB – трапеция с основаниями AB=b и PQ=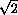 .
.
Пусть T – ортогональная проекция точки P на плоскость основания пирамиды,
а PN – высота трапеции APQB . Тогда точка T лежит на диагонали BD квадрата ABCD , T – середина DH , а TN 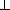 AD по теореме о
трёх перпендикулярах, причём TN =
AD по теореме о
трёх перпендикулярах, причём TN = 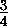 AD =
AD = 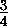 b и PT =
b и PT =
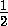 SH =
SH = 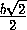 .
.
Из прямоугольного треугольника PTN находим, что
PN = 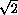 =
=
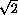 =
=
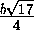 .
.
SAPQB = 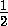 (AB+PQ)· PN =
(AB+PQ)· PN =
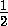 (b+
(b+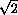 )·
)· 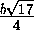 =
=
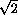 .
.
Ответ
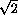 b2.
b2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь