Олимпиадная задача по стереометрии: площадь сечения пирамиды SABC через вершину B
Задача
В основании пирамиды SABC лежит правильный треугольник ABC , а все
боковые грани имеют равные площади. Ребро SA равно 2, ребро SB равно 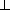 . Через вершину B проведено сечение пирамиды перпендикулярно
ребру SC . Найдите площадь этого сечения.
. Через вершину B проведено сечение пирамиды перпендикулярно
ребру SC . Найдите площадь этого сечения.
Решение
Поскольку боковые грани пирамиды равновелики, а их основания равны как стороны равностороннего треугольника, высоты боковых граней, проведённые из общей вершины S , также равны между собой. Значит, высота SH пирамиды проходит либо через центр вписанной, либо через центр одной из вневписанных окружностей основания ABC , а т.к. по условию задачи пирамида не является правильной ( SA>SB ), то высота проходит через центр H вневписанной окружности, причём эта окружность касается стороны BC и продолжений сторон AC и AB .
Пусть r – радиус этой окружности, сторона основания ABC равна a , M – середина BC . Тогда
HM=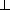 , HA = HM+AM = a
, HA = HM+AM = a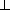 .
.
 AB , значит, HP – радиус
рассматриваемой вневписанной окружности. Из прямоугольных треугольников SHA , SBP и SHP находим, что
AB , значит, HP – радиус
рассматриваемой вневписанной окружности. Из прямоугольных треугольников SHA , SBP и SHP находим, что
SH2 = SA2-HA2 = 4-3a2, SP2 = SB2-BP2 = 2- 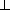 a2,
a2,
SH2 = SP2-HP2 = 2- 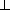 a2-
a2-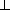 a2 = 2-a2.
a2 = 2-a2.
Пусть BK – высота треугольника SBC со сторонами SB=SC=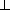 , BC=1. Тогда
, BC=1. Тогда
BK· SC = BC· SM, BK = 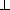 =
=
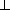 =
=  .
.
SK = 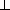 =
=  =
= 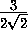 .
.
Пусть отрезки SM и BK пересекаются в точке E . Прямая BC перпендикулярна плоскости AMS , значит, LE  BC , а т.к. LE
BC , а т.к. LE  SK , то прямая LE перпендикулярна
плоскости SBC , поэтому LE
SK , то прямая LE перпендикулярна
плоскости SBC , поэтому LE  KB , т.е. LE – высота треугольника сечения BKL .
KB , т.е. LE – высота треугольника сечения BKL .
Обозначим  ASM = α . По теореме косинусов
ASM = α . По теореме косинусов
cos α = 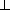 =
=
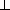 =
= 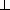 ,
tg α =
,
tg α = 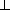 .
.
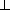 =
=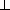 , SE =
, SE = 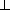 =
=
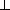 =
=  .
.
 LE ( SK – перпендикуляр к секущей плоскости, KE – ортогональная
проекция наклонной SE ). Из прямоугольного треугольника SEL находим, что
LE ( SK – перпендикуляр к секущей плоскости, KE – ортогональная
проекция наклонной SE ). Из прямоугольного треугольника SEL находим, что
LE = SE· tg α =
 ·
· 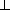 =
=
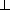 .
.
SΔ BKL = 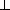 BK· LE =
BK· LE =
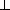 ·
·  ·
· 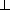 =
=
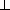 .
.
Ответ
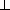 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь