Олимпиадная задача по планиметрии: выпуклые четырёхугольники с равными суммами синусов

Обозначим через α , β , γ и δ последовательные углы четырёхугольника. По условию задачи sin α+ sin γ = sin β + sin δ , а т.к. α+β+γ+δ = 360^o , то sin δ= sin (360^o -α-β -γ)=- sin (α+β +γ), поэтому sin α+ sin γ = sin β - sin (α+β +γ).

Преобразуем это равенство, применяя формулы тригонометрии.

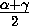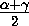2 sin cos = -2 sin 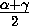cos (β + ),

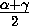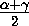Заметим, что α+γ 360^o , поэтому sin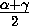 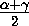0, значит,

cos =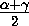

• cos (β + 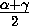), cos 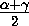+ cos (β + 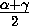)=0,

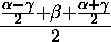2 cos cos 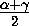, cos cos 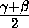= 0,

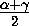откуда находим, что cos =0или cos 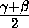=0, значит, α+β = 180^o или γ+β=180^o , а т.к. углы α и β прилежат к одной стороне четырёхугольника, то в первом случае две противоположные стороны парараллельны, а во втором – две другие. Следовательно, четырёхугольник – либо трапеция, либо параллелограмм.

Параллелограмм или трапеция.