Олимпиадная задача по планиметрии: площади вписанных правильных многоугольников
Задача
В окружность вписаны три правильных многоугольника, число сторон каждого последующего вдвое больше, чем у предыдущего. Площади первых двух равны S1 и S2. Найдите площадь третьего.
Решение
Пусть S – площадь третьего многоугольника, R – радиус окружности, n – число сторон первого многоугольника, α = π/2n. Тогда S1 = ½ nR² sin 4α,
S2 = nR² sin 2α, S = nR² sin α = S2/cos α. Из первых двух равенств S1/S2 = cos 2α значит, 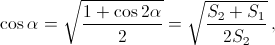
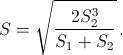
Ответ
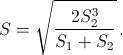
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет