Олимпиадная задача по планиметрии: многоугольники, окружность и периметры для 8-9 класса
Задача
Два правильных многоугольника с периметрами a и b описаны около окружности, а третий правильный многоугольник вписан в эту окружность. Второй и третий многоугольники имеют вдвое больше сторон, чем первый. Найдите периметр третьего многоугольника.
Решение
Пусть R – радиус окружности, x – периметр третьего многоугольника, n – число сторон первого многоугольника. Обозначим α = π/n. Тогда
a = 2nR tg 2α, b = 4nR tg α, x = 4nR sin α = b cos α.
Отсюда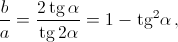 
значит, 
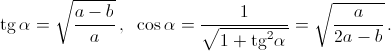Следовательно,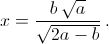 
Ответ
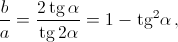
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет