Олимпиадная задача по стереометрии: общая часть пирамиды и тетраэдра для 10-11 классов
Задача
Объём правильной четырёхугольной пирамиды SABCD равен V . Высота SP пирамиды является ребром правильного тетраэдра SPQR , плоскость грани PQR которого перпендикулярна ребру SC . Найдите объём общей части этих пирамид.
Решение
Обозначим AB = a ,  SCP = α . Пусть плоскость,
проходящая через прямую BD перпендикулярно ребру SC пирамиды SABCD , пересекает это ребро в точке H (рис.1). Высота SP пирамиды SABCD является ребром правильного тетраэдра SPQR , а высота
тетраэдра лежит на прямой SC . Поэтому плоскость грани PQR тетраэдра проходит через точку P перпендикулярно SC , а
значит, совпадает с плоскостью BDH . Следовательно, SH – высота
правильного тетраэдра SPQR .
SCP = α . Пусть плоскость,
проходящая через прямую BD перпендикулярно ребру SC пирамиды SABCD , пересекает это ребро в точке H (рис.1). Высота SP пирамиды SABCD является ребром правильного тетраэдра SPQR , а высота
тетраэдра лежит на прямой SC . Поэтому плоскость грани PQR тетраэдра проходит через точку P перпендикулярно SC , а
значит, совпадает с плоскостью BDH . Следовательно, SH – высота
правильного тетраэдра SPQR .
Отрезок PH – высота прямоугольного треугольника SPC , проведённая
из вершины прямого угла, поэтому  SPH =
SPH =  SCP = α , а
т.к. SPH – угол между ребром SP правильного тетраэдра и гранью PQR , то
SCP = α , а
т.к. SPH – угол между ребром SP правильного тетраэдра и гранью PQR , то
cos α = cos  SPH =
SPH = 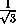 ,
sin α =
,
sin α = 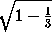 =
= 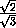 ,
tg α =
,
tg α = 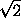 .
.
SP = CP tg α = 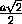 ·
· 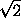 = a,
= a,
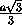 .
.
Рассмотрим сечение пирамиды и тетраэдра плоскостью BDH . Получим равнобедренный
треугольник BDH с основанием BD=a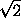 и высотой HP =
и высотой HP = 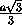 ,
и равносторонний треугольник PQR . Обозначим
,
и равносторонний треугольник PQR . Обозначим  BHP = γ . Тогда
BHP = γ . Тогда
tg γ = 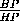 =
= 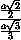 =
=
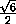 ,
cos γ =
,
cos γ = 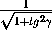 =
=
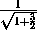 =
=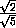 ,
sin γ =
,
sin γ = 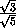 .
.
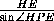 =
= 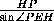 ,
,
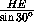 =
=  ,
,
HE = 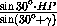 =
=
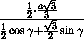 =
=
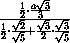 =
=
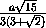 .
.
sin  PEH = sin γ =
PEH = sin γ = 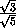 >
>
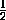 = sin 30o = sin
= sin 30o = sin  HPE,
HPE,
PE < HE = 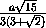 < a=PQ.
< a=PQ.
= 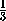 SSPEHF· SH =
SSPEHF· SH =
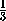 · 2SΔ HEP· SH =
· 2SΔ HEP· SH =
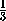 · 2·
· 2· 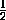 HP· HE sin γ · SH =
HP· HE sin γ · SH =
=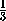 ·
· 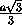 ·
· 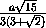 ·
·
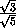 · a
· a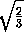 =
=
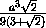 .
.
V = 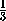 SSABCD· SP =
SSABCD· SP =
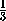 a2· a =
a2· a = 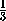 a3,
a3,
V1 =a3· 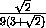 =
3V·
=
3V· 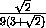 =
= 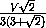 =
=
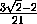 V.
V.
Ответ
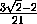 V .
V .
Чтобы оставлять комментарии, войдите или зарегистрируйтесь