Олимпиадная задача по стереометрии: объём пересечения двух цилиндров (10–11 класс)
Задача
Найдите объём общей части двух прямых круговых цилиндров радиуса a , пересекающихся под прямым углом (т.е. их оси пересекаются под прямым углом).
Решение
Проекция пересечения P цилиндров на плоскость, перпендикулярную оси одного из цилиндров, есть круг радиуса a . Половина тела P изображена на рис.1. При этом ABCD – квадрат со стороной2a . Если "вкатить" шар S радиуса a в каждый из цилиндров, то он будет вписан в тело P . Сечение этого тела плоскостью, параллельной ABCD , есть квадрат, а сечение этой же плоскостью шара S – круг, вписанный в этот квадрат.
Если сторона квадрата равна b , то радиус вписанного в него круга
равен 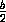 (рис.2), поэтому отношение площадей квадрата и круга равно
(рис.2), поэтому отношение площадей квадрата и круга равно 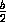 =
= 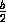 .
.
Из принципа Кавальери следует, что объём V тела P в 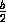 раз
больше объёма шара S , т.е.
раз
больше объёма шара S , т.е.
V = 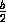 ·
· 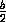 π a3 =
π a3 = 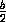 a3.
a3.
Ответ
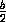 a3.
a3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь