Олимпиадная задача: площадь между параболами и разделяющая вертикальная прямая
Задача
Числа p и q таковы, что параболы y = – 2x² и y = x² + px + q пересекаются в двух точках, ограничивая некоторую фигуру.
Найдите уравнение вертикальной прямой, делящей площадь этой фигуры пополам.
Решение
Если x1 < x2 – абсциссы точек пересечения данных парабол, то для каждого числа x0 из интервала (x1, x2) площадь части исходной фигуры, расположенной слева от вертикальной прямой x = x0, равна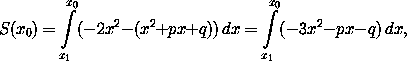 
то есть совпадает с площадью соответствующей части новой фигуры, ограниченной осью абсцисс и параболой y = – 3x² – px – q. Эта парабола пересекает ось x в точках x1, x2, а значит, симметрична относительно прямой x = ½ (x1 + x2). Следовательно, площадь новой фигуры (равно как и исходной) разделится пополам, когда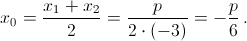 
Ответ
x = – p/6.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь