Олимпиадная задача по планиметрии для 9-11 класса от Заславского А. А.
Задача
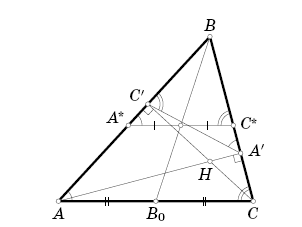
Высоты AA' и CC' остроугольного треугольника ABC пересекаются в точке H. Точка B0 – середина стороны AC.
Докажите, что точка пересечения прямых, симметричных BB0 и HB0 относительно биссектрис углов B и AHC соответственно, лежит на прямой A'C'.
Решение
Как известно, ∠A = ∠BA'C' и ∠BCA = ∠BC'A'. Рассмотрим треугольник ABC, симметричный треугольнику A'BC' относительно биссектрисы угла B (см. рис.). Этот треугольник гомотетичен треугольнику ABC с центром в точке B. Значит, BB0 проходит через середину отрезка AC. Поэтому прямая, симметричная BB0 относительно биссектрисы угла B, проходит через середину отрезка A'C'. AC' и CA' – высоты треугольника AHC. Отсюда, как выше, следует, что прямая, симметричная HB0 относительно биссектрисы угла AHC, также проходит через середину отрезка A'C'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь