Олимпиадная задача по планиметрии: разрезание выпуклой фигуры из дуг окружностей
Задача
Покажите, что существует выпуклая фигура, ограниченная дугами окружностей, которую можно разрезать на несколько частей и из них сложить две выпуклые фигуры, ограниченные дугами окружностей.
Решение
Первое решение. Разрезав криволинейный шестиугольник с дугами в качестве сторон, можно сложить криволинейный "квадрат" и линзу (рис.).
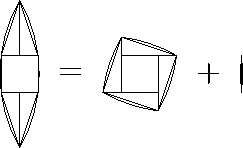
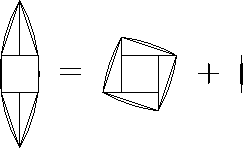
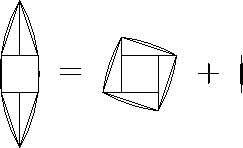
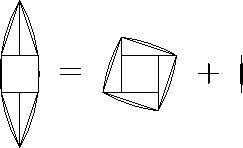
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет