Олимпиадная задача по планиметрии для 8–9 класса: биссектриса, центр окружности и перпендикулярность
Задача
Пусть AL – биссектриса треугольника ABC, O – центр описанной около этого треугольника окружности, D – такая точка на стороне AC, что AD = AB. Докажите, что прямые AO и LD перпендикулярны.
Решение
Обозначим угол B через β (см. рис.). Первый способ. Пусть β < 90°. Тогда ∠AOC = 2β. Поскольку треугольник ACO равнобедренный, ∠OAC = 90° – β. Треугольники ABL и ADL равны по двум сторонам и углу между ними, поэтому ∠ADL = β. Обозначим точку пересечения AO и DL через S. ∠SAD + ∠SDA = 90°, так что треугольник ASD прямоугольный.
Случай β > 90° рассматривается аналогично: ∠SAD = β – 90°, ∠SDA = 180° – β.
В случае β = 90° точка D лежит на луче AO и треугольники ABL и ADL равны, поэтому ∠ADL = 90°.
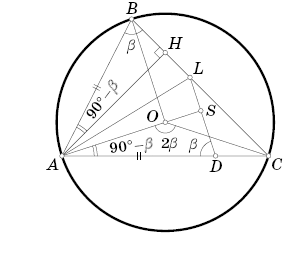
Пусть β > 90°. Тогда ∠HAB = β – 90° = ∠OAC, причём лучи AO и AH лежат вне угла BAC, а значит, также симметричны относительно AL.
В случае β = 90° точка D лежит на AO, и точка H совпадает с точкой B, прямые AO и AB симметричны относительно биссектрисы AL.
Прямые LB и LD симметричны относительно AL, так как треугольники ABL и ADL равны. Значит, угол между прямыми AO и LD равен углу между симметричными им прямыми AH и LB, то есть равен 90°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь