Олимпиадная задача по стереометрии: точка O и параллельные отрезки в тетраэдре
Задача
На грани ABC тетраэдра ABCD взята точка O и через неё проведены отрезки OA1, OB1и OC1, параллельные рёбрам DA , DB и DC , до пересечения с гранями тетраэдра. Докажите, что
+ 
+
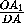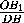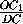= 1.
Решение
Пусть x и h – высоты тетраэдров OBCD и ABCD , опущенные
из вершин O и A соответственно. Тогда 
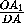= , т.к. наклонные OA1и AD к плоскости грани BCD параллельны. Тогда
=
=
= .
= ,
= .
+ +=
++
=
=
= 
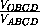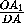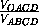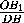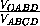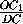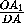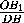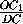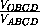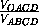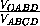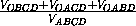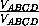= 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет