Докажите свойство расстояний от точки до граней тетраэдра — олимпиадная задача стереометрии
Задача
Докажите, что если x1, x2, x3, x4– расстояния от произвольной точки внутри тетраэдра до его граней, а h1, h2, h3, h3– соответствующие высоты тетраэдра, то
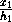 +
+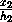 +
+
 +
+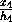 = 1.
= 1.
Решение
Пусть M – точка внутри тетраэдра ABCD , x1– расстояние от этой точки до грани ABC , h1– высота тетраэдра, опущенная из вершины D , V – объём тетраэдра ABCD , V1– объём тетраэдра ABCM . Тогда h1– высота тетраэдра ABCM , опущенная из вершины M , поэтому
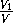 =
= 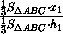 =
= 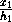 .
.
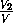 =
=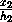 ,
,
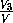 =
= ,
,
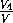 =
=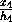 ,
,
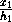 +
+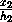 +
+
 +
+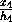 =
=
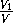 +
+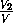 +
+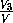 +
+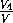 =
=
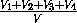 =
= 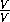 = 1.
= 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет